Projects
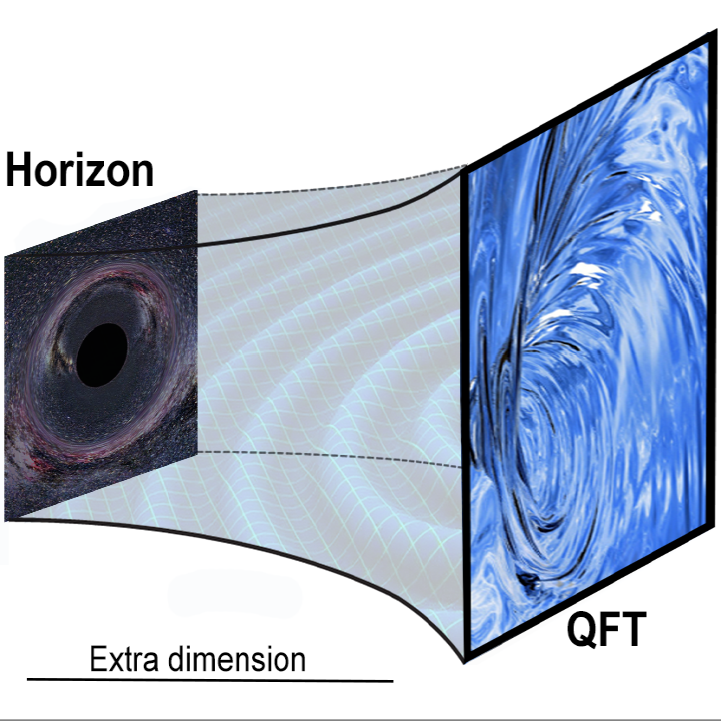
Non-equilibrium dynamics of strongly coupled QFTs from gravity
Martin Ammon
We investigate quantum fields far from equilibrium for strongly coupled systems within the AdS/CFT correspondence by mapping strongly coupled quantum field theories to classical gravitational theories.
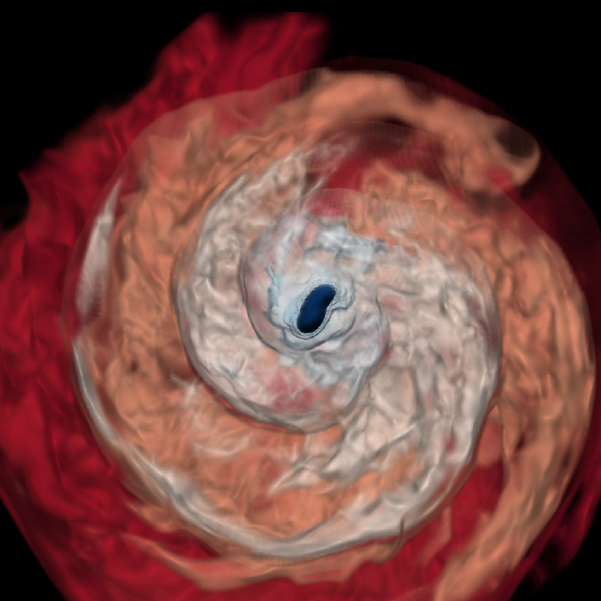
Gravitational waves as probes of strong and dynamical fields
Sebastiano Bernuzzi
Using gravitational waves as probes, we study the general relativistic two-body dynamics in the strong field regime and employ this knowledge to constrain fundamental physics of black holes and of extreme matter fields.

Critical Collapse in General Relativity
Bernd Brügmann
Black holes are a fundamental strong field phenomenon of general relativity. Several important features of black holes are known in analytic or semi-analytic form, but many key features, in particular those related to dynamical spacetimes, are only accessible through numerical simulation. The topic of this project is critical phenomena in gravitational collapse in general relativity.
Quantum energy inequalities and thermal properties of quantum field theory
Daniela Cadamuro
Quantum energy inequalities play an important role in QFT as they are related to the stability of spacetime. In particular, they exclude existence of ``exotic'' spacetime geometries such as wormholes, warp drives and time-machines. We investigate whether Quantum energy inequalities are related to the existence of local thermal equilibrium states and local stability of QFTs.
Critical phenomena in fermionic systems and gravity
Holger Gies
All visible matter in the universe essentially consists of fermions. The masses of these matter building blocks are largely shaped by critical phenomena such as chiral symmetry breaking. We investigate the interplay between fermionic matter, curved (quantized) spacetime, and corresponding mass generating mechanisms possibly active in the early universe.
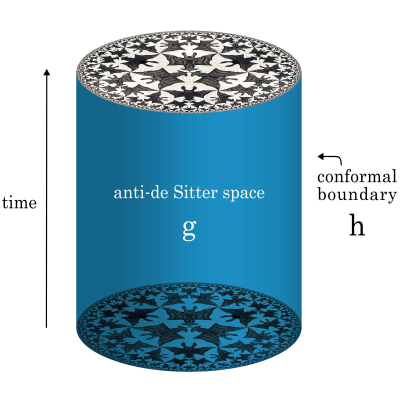
Quantum field theory and gravity on manifolds with boundary
Stefan Hollands
QFTs on space(times) with boundaries are relevant in many contexts, e.g., in the Casimir effect, near defects, junctions, interfaces, topological insulators or even spacetime singularities. It is a goal of this project to set up a general theory of renormalization for models of quantum fields in space(times) with boundaries.
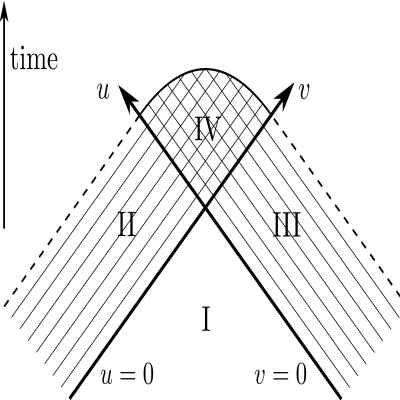
Nonlinear interactions in Einstein-Maxwell theory
Reinhard Meinel
Using the ``inverse scattering method'' - that has been developed in the context of soliton theory and can be applied to the Einstein-Maxwell equations in the presence of two commuting Killing fields - we will study (i) collisions of gravitational and electromagnetic waves and (ii) quasi-stationary routes from ``normal'' matter configurations to black holes in Einstein-Maxwell theory.
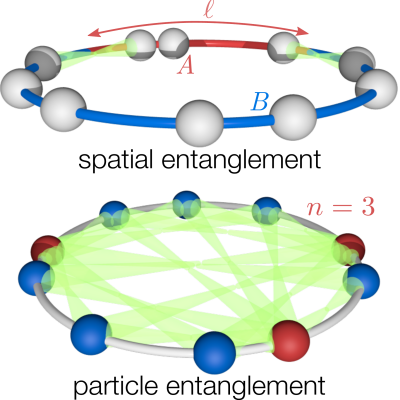
Non-equilibrium bosonization, quantum quenches, and particle entanglement
Bernd Rosenow
A focus of interest are one-dimensional electron systems out of equilibrium and their relaxation towards (non-)equilibrium steady states. We study interaction quenches in systems of fermions, and focus on entanglement entropy characterizing the approach to late-time behavior.
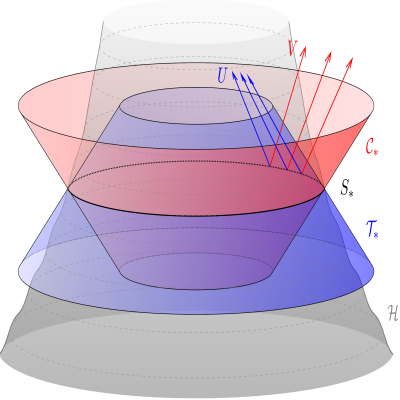
Quantum Fields in Non-equilibrium and Black Hole Evaporation
Rainer Verch
The Hawking effect, predicting radiation by black holes due to quantum effects and correspondingly black-hole evaporation, features the puzzling scenario called ``information loss paradox''. We study the existence of solutions for evaporating back holes of semiclassical gravity to advance the analysis of thermodynamical properties of quantum fields on black-hole spacetimes and a corresponding entropy concept.
Interacting Fermions in external fields, finite temperature and nonzero density
Andreas Wipf
We plan a comprehensive study of the critical behavior, symmetry breaking patters and mass generation in 2 and 3-dimensional fermionic systems (Weyl/Dirac materials) within lattice field theory. Relevant phase transitions are investigated as a function of termperature, density and spacetime curvature.
